Lossless Algorithms

The following is an algorithm I wrote for generating support/resist in trading with no thresholds or parameters. On each price move, the price range traveled loses a point in score. The resulting score of any price range is its support/resist strength, which declines the more it is traveled across (zero being strongest and untraveled). Visually, the price line looks like a long horizontal eraser scrubbing away on a chalkboard; price ranges least scrubbed thin out to support/resist lines.  The reason I call it a "lossless" algorithm is because it doesn't estimate anything or use any seeded values/thresholds.  It is analogous to lossless audio/image file formats.  There is no sampling or use of statistics, just a 1-to-1 map of where price moves most and least freely.  It is also extremely light both in computation and space because all you're doing is a single subtraction per datapoint and the max number of ranges to keep score of is the granularity of your price axis (it pretty much is like an algorithm for drawing an image if anything).


As someone who doesn't like doing too much number crunching, I habitually design my algorithms this way (to not rely on any seeded values, parameters, or numbers in general).  This is in contrast to more common quants/data-scientist approaches, who calculate backwards to a lookback window or threshold.  Not only can that approach end up computationally expensive (by constantly re-sampling the last x datapoints), but the result fundamentally can only ever be an estimate, one that changes depending on assumptions/parameters used - vs here where there aren't any.  People always ask me what numbers I use for lookback window, granularity, thresholds, assumptions, etc, but here those things literally don't exist.  It's a bit like asking for the number of pixels in a vector image; there's no such thing.

I don't go out of my way to avoid having parameters in my algorithms; it just ends up that way when I code for myself.  I never see myself crunching statistics or running some equation in my head in real life, and I try to code my algorithms to go through the same logical processes.

=======================

20210315 Added Note: Since a lot of people, even after reading this, get confused and still think to code this with set parameters, ranges, or other seeded information, here's an example walking through what the code actually would do to check your work:

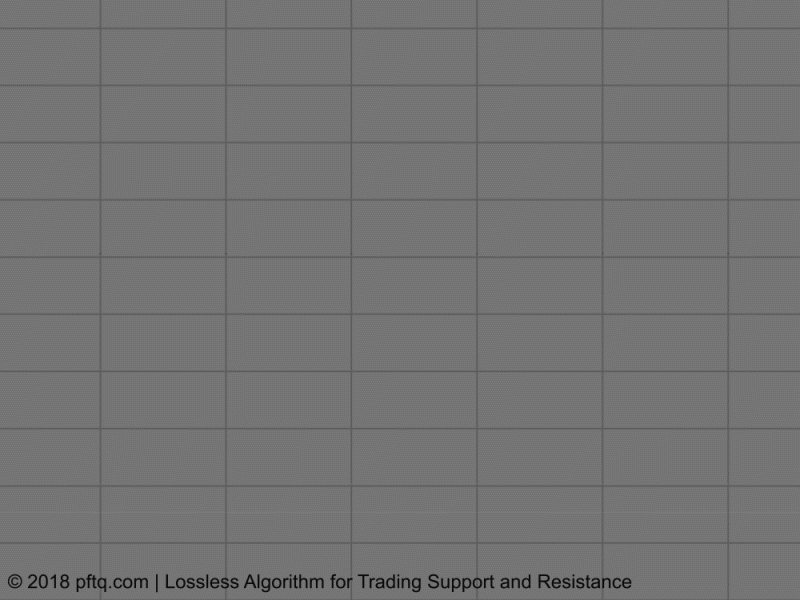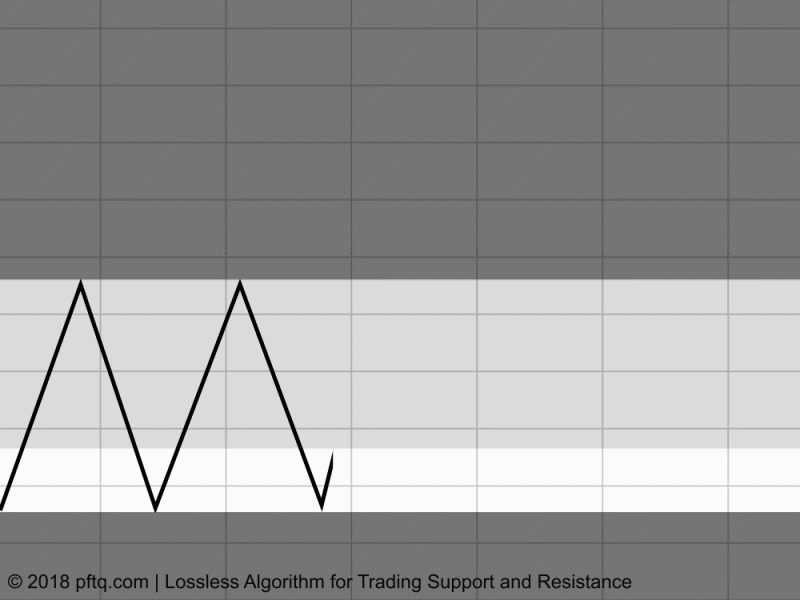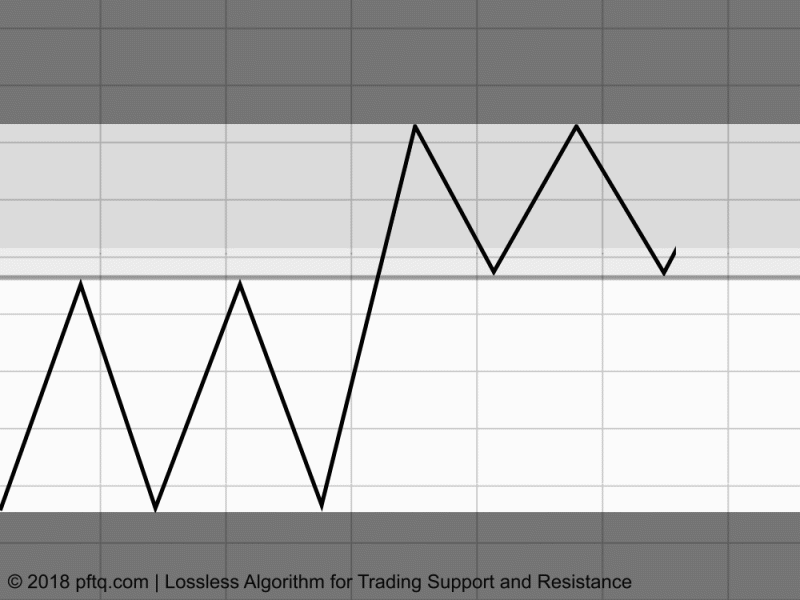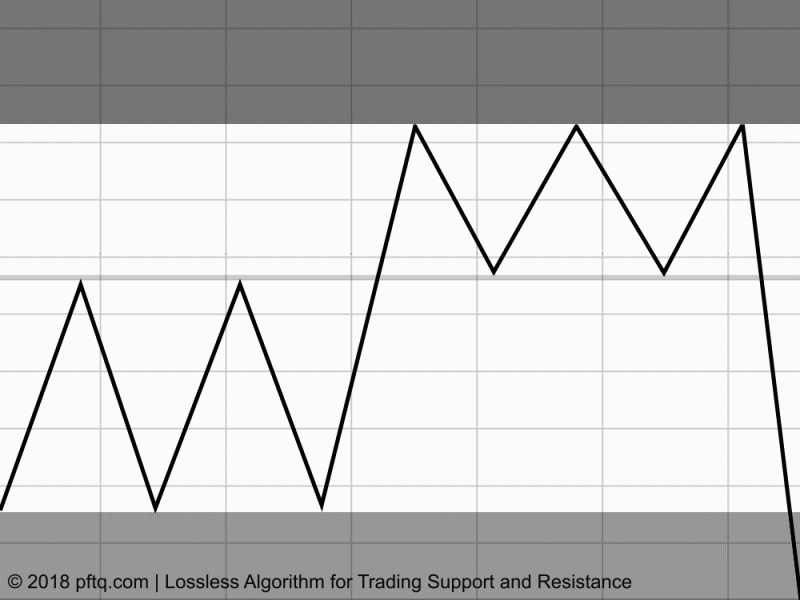
The important part to realize is there are no actual line objects coded - support and resistance are just interpretations by the person looking at the chart.  The code itself just shades a canvas white based on how often any particular range has been visited by the price, and the remaining least shaded areas are what we perceive as lines (even though they don't "exist" in the code).

If it crosses from $9-10, that's a score of -1, and the shading of that range is white with opacity of 10%.
If it crosses back down from $10 to $9, the score is -2 and the opacity increases to 20%.
It crosses from $9 to $8.15 for the first time, and that new range is a score of -1, white opacity at 10%.
It crosses back from $8.15 to $10 and the $8.15-9 range score goes to -2, $9-10 score now goes to -3.
Any remaining areas untraveled have a score of 0, leaving "support" and "resistance" areas left dark.

The actual percentage of opacity/shading is arbitrary and purely aesthetic.  The important part is the score that is open-endedly added or subtracted to and does not require any fitting or adjustment.

================

Additional note:

Veritasium's video on the Game of Life algorithm is a similar concept - the idea that you can code something that works perpetually without refinement or parameter adjustment even if you can't empirically prove it:
https://youtu.be/HeQX2HjkcNo?t=65